Álgebra
Esquema de sección
-
-

Las transformaciones son funciones. Si, funciones como las que has estudiado en el nivel medio, en el ingreso o que estás estudiando en Análisis matemático I. Pero te preguntarás: ¿porqué, si son funciones se las llaman Transformaciones?. En realidad, muchas de las funciones que estudiaremos tienen como dominio IR2 y como imagen IR2, por lo que para representarlas gráficamente como has venido graficando funciones, se necesitaría un espacio de 4 dimensiones, lo cual no es posible, por lo que se grafica el dominio en un plano y el codominio en otro plano, de manera que se interpreta como que la función transforma puntos de un plano en puntos del otro plano. De allí que se las llame transformaciones. Son ejemplo de transformaciones las simetrías, las proyecciones, etc. Pero no toda transformación es una transformación lineal. Definamos transformación lineal.

Sean V y W dos espacios vectoriales sobre un mismo cuerpo K. Una función F, definida del espacio V en el espacio W, será una TRANSFORMACIÓN LINEAL, si preserva las operaciones de suma y multiplicación por un escalar definidas en los espacios V y W.

Nota: las condiciones dadas en 1 y en 2 para la determinación de si una función es una transformación lineal, pueden expresarse en una única condición, como sigue:
siendo u y v vectores de V, k1 y k2 escalares reales.
En general, a las transformaciones lineales las denotaremos como:
T: V →W tal que T(v) = w,
de modo que la función T asigna a cada elemento v del espacio V una imagen w del espacio W. Se dice que w es la imagen del vector v bajo T y se indica T(v)=w , también se suele decir que es el transformado de v. Además, como T es una función, se dice que V es el dominio de T y W es el codominio de T.
Importante:
• ¿Qué significa que las Transformaciones lineales TL preservan las operaciones de suma de vectores y multiplicación por un escalar?
Que preserve la suma de vectores, significa que obtendremos el mismo resultado si primero sumamos dos vectores u y v del dominio de T y al vector suma le aplicamos la TL , que si primero le aplicamos la TL a u y a v y luego sumamos los vectores transformados.
Que preserve la multiplicación por un vector significa que obtendremos el mismo resultado si primero multiplicamos el vector u del dominio de T por un escalar k y luego le aplicamos la TL , que si primero le aplicamos la TL a u y luego multiplicamos el transformado de u por el escalar k.
• Si una transformación lineal está definida de un espacio vectorial V en el mismo espacio V, se denomina operador lineal.
-
-

Son Transformaciones lineales algunas transformaciones del plano como:
LAS SIMETRÍAS AXIALES: (simetrías respecto de un eje)
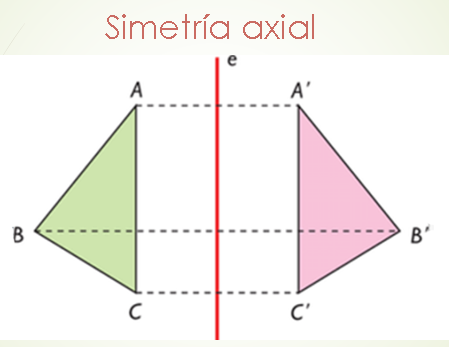
El triángulo ABC está formado por puntos del dominio que mediante la Simetría respecto del eje e, se transforma en el triángulo A'B'C'. Más precisamente al punto A del dominio le corresponde como simétrico el punto A'; al punto B le corresponde como image el punto B´ y al punto C, el punto C´.
LAS SIMETRÍAS RADIALES:
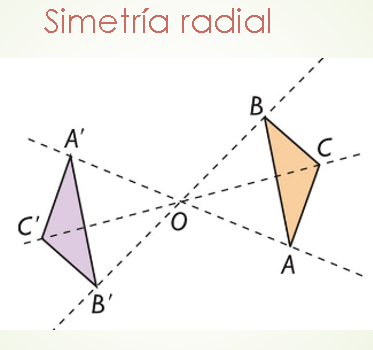
El triángulo ABC está formado por puntos del dominio que mediante la Simetría respecto del punto O, se transforma en el triángulo A'B'C'. Más precisamente al punto A del dominio le corresponde como simétrico el punto A'; al punto B le corresponde como image el punto B´ y al punto C, el punto C´.
LAS HOMOTECIAS
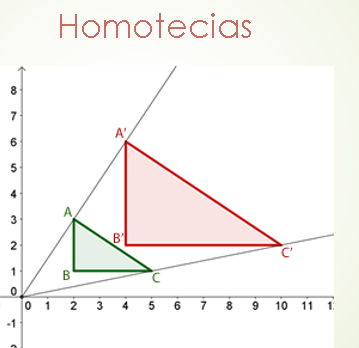
En este caso, la homotecia agranda al triángulo ABC y lo transforma en el triángulo A'B'C'.
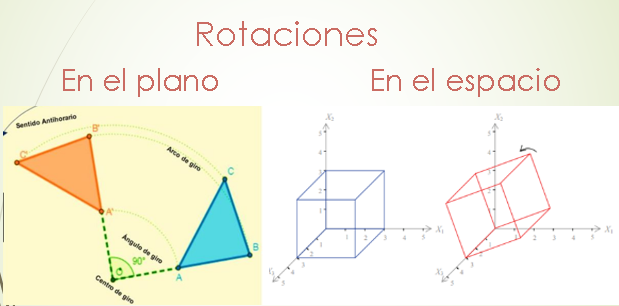
Las rotaciones, tanto en el plano como en el espacio son ejemplos de transformaciones lineales.
Las transformaciones también están presentes en la vida real. Por ejemplo:

Las reflexiones son transformaciones lineales.

Cuando agrandamos una foto o imagen, estamos aplicando una homotecia que ya dijimos que es una transformación lineal.

Las proyecciones también son ejemplos de transformaciones lineales.
-